Daly Detector | Ion Counting

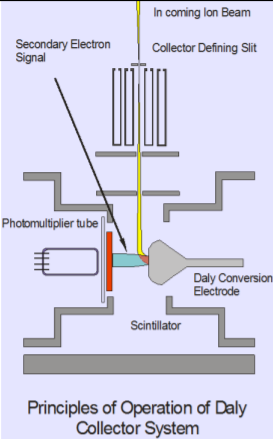
The Daly detector was designed by N.R Daly in the 1960’s . The design uses a conversion dynode to convert incident ions into electrons. It also separates the multiplication electronics away from the ion beam preventing secondary ion production on the multiplication dynodes.

The conversion surface is a highly polished, aluminised metal surface that is biased at ~25KV. The bias voltage controls the peak shape and to some extent the transmission. However, the efficiency variation is very small above 20KV.

Ions impact onto the Daly conversion electrode which releases electrons.These are repelled onto a scintillator forming photons. The photons are detected by a photomultiplier which is external to vacuum. This is radically different to an electron multiplier where the active surface of the multiplier is in the line of sight of the ion beam and the multiplication stages are all in vacuum.

The photomultiplier used is a Hamamatsu tube SN R6247, which replaces the earlier Photonis XP2900 tubes. Substantial modifications to the ion counting electronics have been made to ensure the multiplication electronics and discrimination are close coupled to the tube, this has eliminated “ringing” and double counting.

Principles of Operation of Daly Collector System

Introduction

Ion counting detectors are used to measure extremely small ion currents typically between 1e^-16 and 1e^-13amps. For applications that involve large isotope ratios such as uranium or radiogenic lead, or indeed for zircon geochronology where the Pb contents of individual zircons is extremely variable, it is crucial that ion-counting detectors have a linear response.

Non linearity of ion-counters is due to a combination of factors which have been discussed at length in the literature (e.g. Richter et. al 2001). Potentially the largest source of error is the calibration of the deadtime (DT).

The deadtime is the period after a count has been registered before another ion can be counted and ideally it should be constant irrespective of count rate.

Typically the DT is a few tens of nanoseconds but it must be measured accurately to minimize its affects at high count rates. For example a count rate of 1e⁶ cps equates to a time between counts of 1 microsecond and a 10ns deadtime would be a 1% contribution.

Richter et. al. have shown that at count rates greater than ~20,000 cps, Secondary Electron Multipliers (SEM’s) are non-linear even after DT correction . The non-linearity becomes larger at higher count rates and can be as high as 1% at 6e⁵ cps.v

Ion-Counting Daly Detector

The main axial ion-counting system used on all Isotopx TIMS instruments is an ion-counting Daly detector. The principle of operation is described in the box above.

The Daly detector offers a number of advantages over SEM type ion-counters. It has a large dynamic range, providing several orders of magnitude overlap with the Faraday collectors. It has the highest gain stability relative to the Faraday collectors, and the largest working peak flat. Several Daly systems have been in continuous operation for over twenty years without replacement of any component.

The Daly on Phoenix and Phoenix X62 TIMS represents the next generation of ion-counting detector. Isotopx have re-designed the Daly to take advantage of the latest developments in photo-multipliers and in counting electronics.

Compared to earlier Daly units this new system has lower noise and a larger dynamic range. The issue of ‘ringing’ has been eliminated which, combined with lower noise, allows a significantly more efficient rejection of false counts.

The purpose of this note is to demonstrate the improved performance of this new Daly system.

Method

The isotopic standard NBS U500 was measured by peak jumping ²³⁴U, ²³⁵U, ²³⁶U and ²³⁸U on the ion-counting Daly detector. The isotope ratios ²³⁴U/²³⁸U and ²³⁶U/²³⁸U are corrected for mass fractionation using ²³⁵U/²³⁸U.

The certified ratio of ²³⁵U/²³⁸U is 0.99968 hence ²³⁵U and ²³⁸U are essentially the same size. Consequently any detector non-linearity will be cancelled out when a ratio is calculated. This means that a fractionation correction applied using ²³⁵U/²³⁸U will have no effect on any detector non-linearity that might be present on other isotope ratio’s.

The sample was loaded onto the side filament of a triple filament and the intensity adjusted by controlling the side filament current. Measurements were made at different intensities of 238U over the course of several days. Each analysis took a minimum of 2 hours, and this was increased for the lower count rate measurements in order to obtain the required precision for the minor isotopes. Isotopes were also simultaneously detected on the off – axis Faraday collectors, such that the Faraday/Daly gain could be determined at different count rates. Table 1 shows the analytical sequence.

	Cycle 1	Cycle 2	Cycle 3	Cycle 4
H4 Faraday	238
H3 Faraday		238
H2 Faraday
H1 Faraday	235
Daly	234	235	236	238

Table 1. Sequence Used

The analysis consists of peak jumping 234, 235, 236 and 238 on the Daly. Integration times are 5 second, 3 second, 5 second and 3 second respectively. In cycle 1, ²³⁵U and ²³⁸U are measured on the off axis Faradays.

The results are shown in Appendix 1. A deadtime of 39.5ns was used for all the data.

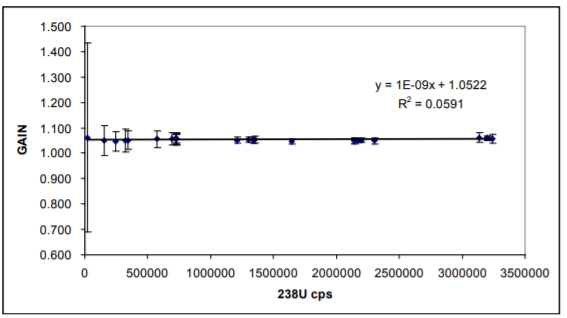
Faraday/Daly Gain

The Faraday/Daly gain was determined by measuring the ²³⁵U/²³⁸U on the Faraday collectors in the first cycle, and 235Daly/238F in the second cycle. Cycle 1 is divided by cycle 2, to obtain the gain.

The data shows that relative to the Faraday collector the Daly is 94.8% efficient and this efficiency remains constant from 24,000 cps of ²³⁸U to >3e6 cps of ²³⁸U (Figure 1).

Figure 1 also gives a good indication of how linear the Daly is. If we assume that the Faraday is linear then there is no change in Daly gain from 24,000 cps of ²³⁸U to >3e6 cps of ²³⁸U. Determining the linearity at low count rates is difficult because of the noise of the Faraday collectors.

Figure 1. Stability and linearity of the Faraday/Daly gain.

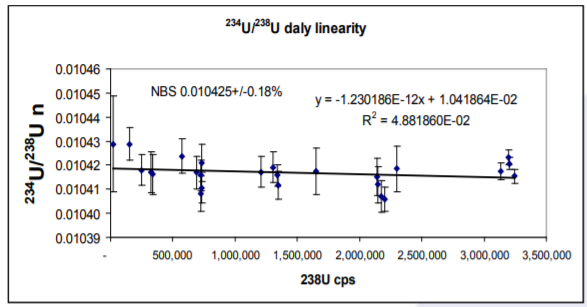
Daly Linearity – ²³⁴U/²³⁸U

²³⁴U/²³⁸U data are shown in Appendix 1 and Figure 2. The average of all the determinations is 0.010417+/- 0.11% 2 RSD. The dynamic range covered is 252cps ²³⁴U to 3.2e⁶ cps ²³⁸U. The mean ratio compares to the reference value of 0.010425 which has an error of approximately 0.2%. The mean accuracy is 0.08%, so the results are within error of the certified value. A linear regression line through the data produces an intercept of 0.010419. The slope of the regression line is 1e^-12, confirming that the Daly is completely linear with one deadtime correction.

Figure 2. Linearity of Daly using ²³⁴U/²³⁸U

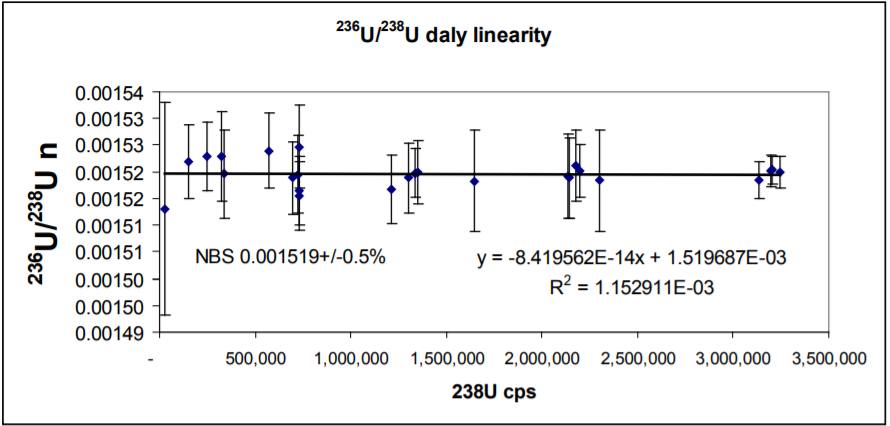
Daly Linearity – ²³⁶U/²³⁸U

²³⁶U/²³⁸U are also shown in Appendix 1 and Figure 3. The ratio is more extreme than the ²³⁴U/²³⁸U. The average of the determinations is 0.001520±0.34% 2RSD. The lowest ²³⁶U determined is 37cps. The regression line through the data shows zero slope, and so the Daly is totally linear with the one deadtime correction. The intercept is indistinguishable from the reference value.

Comparison with SEM detectors.

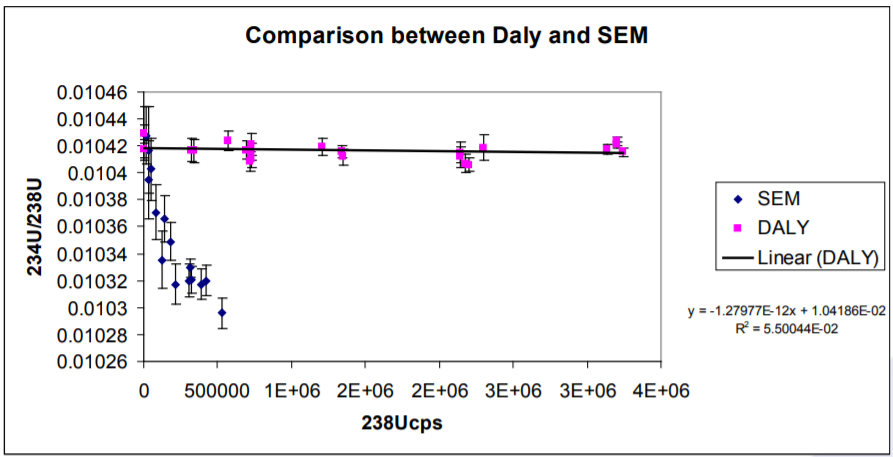
Richter et al 2001, compared a number of SEM detectors commonly used on isotope ratio MS instruments. They showed that a single deadtime correction could not be applied to SEM detectors and an empirical ‘best fit’ curve must first be determined and then applied to acquired data. This became more important for counting rates above 20,000cps as above this level the non-linearity of the SEM’s under test became significant.

The results for ²³⁴U/²³⁸U presented here are compared with those of Richter et. al 2001 in Figure 4. The difference in behaviour between the Daly and an SEM is very clear and highlights the significant benefits of the Daly system over the SEM’s tested by Richer et al.

Figure 3. Linearity of the Daly for ²³⁶U/²³⁸U

Figure 4. Comparison between Daly detector and SEM data from Richter et al 2001.

Reference. S. Richter. Goldberg,S.A, Mason, P.B., Traina, A.J. Schweiters, J.B. 2001. Linearity tests for secondary electron multipliers used in isotope ratio mass spectrometry. International. Journal of Mass Spectrometry. 206. 105-127.

238U cps	236U cps	235U cps	234U cps	235F/238F	235D/ 238F	F/D gain	2RSD	236/ 238N	2se	234/ 238N	2se	235/238
2,300,847	3,488	2,299,970	23,991	1.001545	0.955067	1.049	0.01	0.001518	0.000002	0.010418	0.000010	0.999331
1,646,616	2,514	1,673,888	17,417	1.001710	0.956091	1.048	0.01	0.001518	0.000002	0.010417	0.000010	1.001775
2,138,661	3,247	2,139,792	22,289	1.001320	0.954276	1.049	0.01	0.001519	0.000001	0.010415	0.000008	1.000139
2,144,208	3,259	2,145,036	22,346	1.000974	0.953768	1.049	0.01	0.001519	0.000001	0.010412	0.000008	0.999917
2,176,005	3,312	2,176,720	22,655	1.000401	0.952862	1.050	0.01	0.001521	0.000002	0.010407	0.000007	1.000223
2,201,037	3,348	2,201,669	22,912	1.000659	0.952398	1.051	0.01	0.001520	0.000001	0.010406	0.000005	1.000022
1,209,654	1,836	1,209,526	12,606	1.000119	0.951094	1.052	0.01	0.001517	0.000002	0.010417	0.000006	0.999601
1,302,670	1,981	1,302,574	13,561	1.000557	0.950850	1.052	0.01	0.001519	0.000002	0.010419	0.000006	0.999888
1,338,484	2,033	1,338,285	13,946	1.000241	0.950465	1.052	0.01	0.001520	0.000001	0.010416	0.000004	1.000097
1,348,291	2,050	1,348,249	14,047	1.000562	0.950138	1.053	0.01	0.001520	0.000001	0.010412	0.000006	1.000410
573,048	876	572,910	5,974	1.000650	0.948160	1.055	0.03	0.001524	0.000003	0.010424	0.000007	0.999613
693,130	1,052	693,151	7,216	1.000167	0.946925	1.056	0.02	0.001519	0.000002	0.010417	0.000007	0.999860
723,041	1,098	722,907	7,530	1.001139	0.947547	1.057	0.02	0.001520	0.000002	0.010408	0.000007	1.000676
727,370	1,105	727,838	7,583	1.000013	0.947264	1.056	0.02	0.001516	0.000002	0.010416	0.000006	1.000503
728,951	1,106	729,341	7,598	1.000956	0.946785	1.057	0.02	0.001515	0.000002	0.010411	0.000006	1.000574
729,484	1,112	729,564	7,608	1.000039	0.946270	1.057	0.02	0.001525	0.000002	0.010421	0.000008	1.000114
3,243,170	4,934	3,246,265	33,842	1.000596	0.945347	1.058	0.02	0.001520	0.000001	0.010415	0.000003	1.000917
3,200,796	4,869	3,202,223	33,391	1.000261	0.943679	1.060	0.01	0.001520	0.000001	0.010421	0.000003	1.000708
3,198,439	4,864	3,198,964	33,356	1.000294	0.942507	1.061	0.01	0.001520	0.000001	0.010423	0.000003	1.000239
3,133,163	4,835	3,131,890	32,977	1.000067	0.941618	1.062	0.02	0.001518	0.000001	0.010418	0.000003	1.000038
322,025	491	321,859	3,357	0.999749	0.952248	1.050	0.04	0.001523	0.000002	0.010417	0.000008	0.999855
339,907	516	339,769	3,541	1.001200	0.952472	1.051	0.04	0.001520	0.000003	0.010416	0.000008	0.999828
246,708	376	246,676	2,570	0.999226	0.954233	1.047	0.04	0.001523	0.000002	0.010418	0.000006	0.999871
151,784	231	151,859	1,583	1.001658	0.954366	1.050	0.06	0.001522	0.000002	0.010429	0.000007	1.000495
24,144	37	24,169	252	1.001342	0.942845	1.062	0.37	0.001513	0.000007	0.010429	0.000020	1.001019


					MEAN	1.054		0.001520		0.010417		1.000197
					1SD	0.0046		0.000003		0.000006		0.000528
					2RSD	0.9%		0.34%		0.11%		0.11%
					NBS			0.001519		0.010425
					ACCURACY			0.04%		0.08%

Appendix 1 . U500 isotope ratios measured on the Daly at different intensities

Download the Technical Note

You can download the full Application Note as a PDF: An Assessment of the Linearity of the Ion-Counting Daly Detector and Hamamatsu Photomultiplier Using NBS U500

Discover Isotopx’s Phoenix TIMS

If you would like to find out more about the Phoenix TIMS, please don’t hesitate to contact us. A member of our sales team will be happy to help.

Stay In Touch

If you wish to keep up to date with our products, research and news why not sign up to our infrequent newsletter below. You can also follow us on social media.

An assessment of the linearity of the ion-counting Daly detector and Hamamatsu photomultiplier using NBS U500